Holding Time Maximization Preserving Output Perormance for Timed Event Graphs

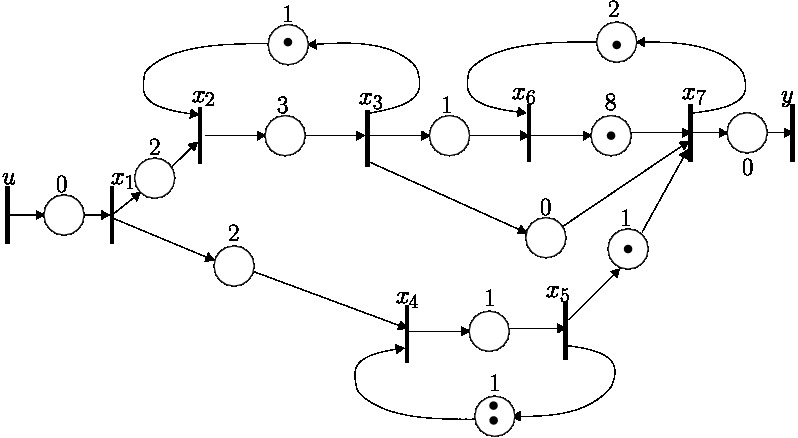
The considered TEG is represented on the figure below:

The state-space model of the previous TEG in Maxin[[γ,δ]] is:

A=
| ε ε ε ε ε ε ε |
| δ2 ε γδ ε ε ε ε |
| ε δ3 ε ε ε ε ε |
| δ2 ε ε ε γ2δ ε ε |
| ε ε ε δ ε ε ε |
| ε ε δ ε ε ε γδ2 |
| ε ε e ε γδ γδ8ε |

B=
| e|
| ε|
| ε|
| ε|
| ε|
| ε|
| ε|

C=
| ε ε ε ε ε ε e |

After holding time maximization, the modified TEG is represented on the figure below:

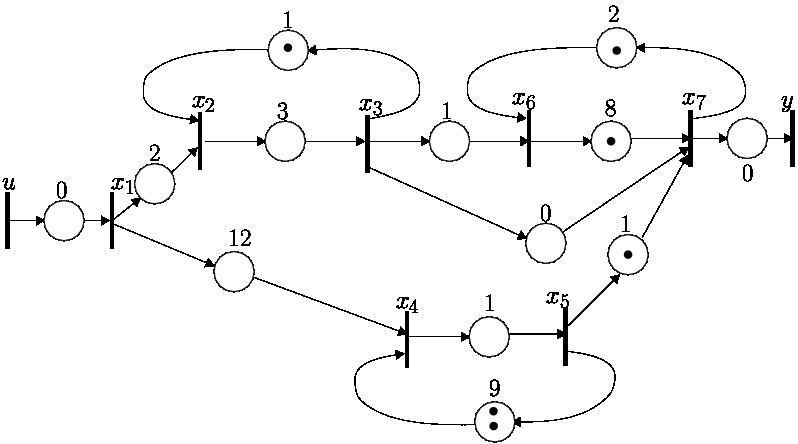
The state-matrix Aopt of the modfied system is:

Aopt = PrγA(CA*\CA*) =
| ε ε ε ε ε ε ε |
| δ2 ε γδ ε ε ε ε |
| ε δ3 ε ε ε ε ε |
| δ12 ε ε ε γ2δ9 ε ε |
| ε ε ε δ ε ε ε |
| ε ε δ ε ε ε γδ2 |
| ε ε e ε γδ γδ8ε |

Code Source of the example considered :


The software is the library Minmaxgd extended with the γ-projection along a series.

The following file contains the extended library and the implementation of the examples of the paper: HolTMax.zip

Original library is available here : Minmaxgd



Date : December 15th, 2012